An exponential encounter
I recently learned about a neat technique, invented by John von Neumann, for generating random samples from an exponential distribution (probability density $e^{-x}$). The algorithm can be generalized to sample from a normal distribution. One notable feature of von Neumann's approach, in addition to its simple brilliance, is that no logarithms are involved in the computation. While this algorithm is now mainly of historical interest, it's still a fun exercise in probability and computation. Here, I'll walk through von Neumann's reasoning and present the algorithm.
A decreasing trend
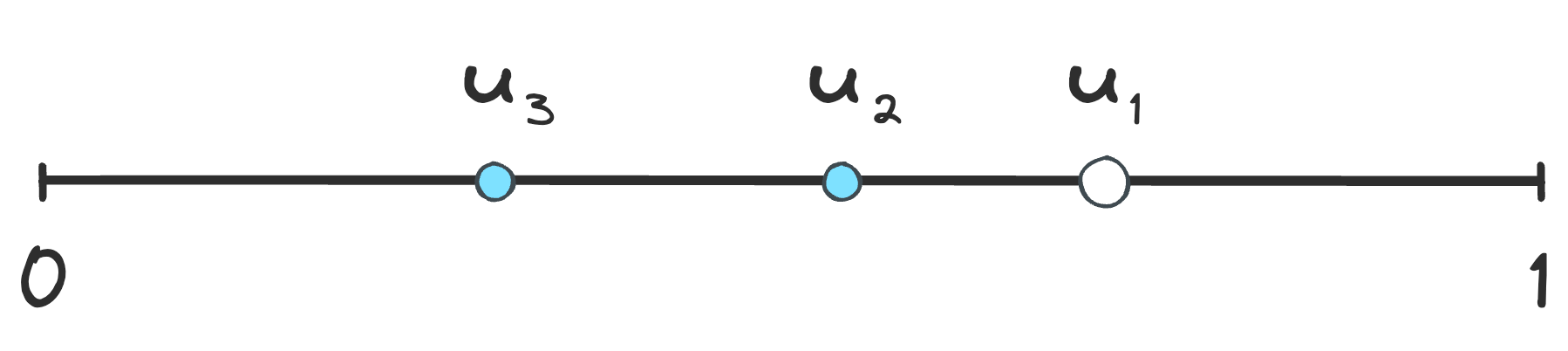
Generate a random number $u_1$ from a uniform distribution over the unit interval $(0, 1)$. The probability that $u_1$ has a value in the infinitesimal range $(u_1, u_1 + du_1)$ is $du_1$. Now pick a second random number $u_2$ in exactly the same way. Given the value of $u_1$, what is the probability that $u_1 > u_2$? Call this probability $P_2(u_1)$. For the inequality to hold, $u_2$ must have a value from 0 to $u_1$, and so the probability is
$$
\begin{equation}
P_2(u_1) = \int_{0}^{u_1} du_{2} = u_1~.
\end{equation}
$$
Choose a third number $u_3$. What is the probability $P_3(u_1)$ that $u_1 > u_2 > u_3$? When $u_1$ is fixed, $u_2$ can take any value from 0 to $u_1$. Similarly, given $u_2$, the value of $u_3$ is between 0 and $u_2$. The probability that $u_1 > u_2 > u_3$ is then
$$
\begin{equation}
P_3(u_1) = \int_{0}^{u_1} du_{2} \int_{0}^{u_2} du_{3} = \frac{u_1^2}{2}~.
\end{equation}
$$
A pattern is starting to emerge!
For any $n$, the probability that $u_1 > u_2 > \ldots > u_n$ is
$$
\begin{equation}
P_n(u_1) = \frac{u_1^{n - 1}}{(n - 1)!}~.
\end{equation}
$$
We've already seen that this holds for $n = 2$ and 3. Apply inductive reasoning to prove it for all $n$. Here's the inductive step:
$$
\begin{align}
P_{n + 1}(u_1)
&= \int_{0}^{u_1} du_{2} \int_{0}^{u_2} du_{3} \ldots \int_0^{u_n} du_{n + 1} \\
&= \int_{0}^{u_1} du_{2} \left[ \int_{0}^{u_2} du_{3} \ldots \int_0^{u_n} du_{n + 1} \right] \\
&= \int_0^{u_1} du_2\, P_n(u_2)~. \\
&= \int_0^{u_1} du_2\, \frac{u_2^{n - 1}}{(n - 1)!} \\
&= \frac{u_1^n}{n!}~. \\
\end{align}
$$
Mathematically, it seems that $P_1(u_1) = 1$. The probabilisitic justification is that a sequence with only $u_1$ is already in order, and the probability is 1 for a decreasing sequence with $n = 1$.
A decreasing trend at its end
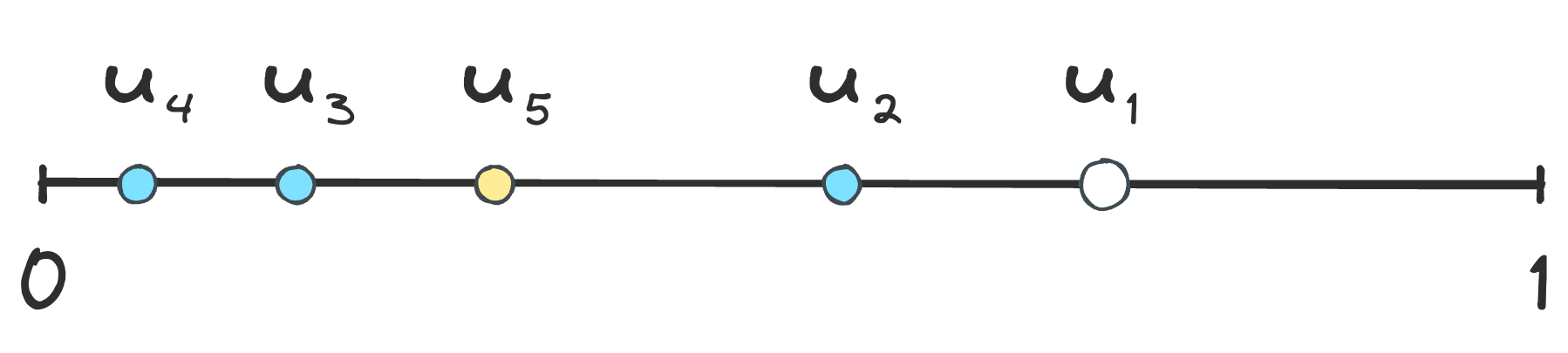
Because $n!$ increases rapidly with $n$, the probability of generating a long decreasing sequence is low. We expect to quickly encounter a number that is out of order. What is the probability that a decreasing sequence terminates after $n$ random draws? This is the joint probability that $u_1 > \ldots > u_n$ and $u_n \le u_{n + 1}$, where the last number, $u_{n + 1}$, ends the decreasing trend. Denote this probability by $S_n(u_1)$ and write it as
$$
\begin{equation}
S_n(u_1) = \int_0^{u_1} du_1 \ldots \int_0^{u_{n-1}} du_n \int_{u_n}^1 du_{n + 1}~.
\end{equation}
$$
After some simple manipulation, we find
$$
\begin{align}
S_n(u_1) &= ~ \int_0^{u_1} du_1 \ldots \int_0^{u_{n-1}} du_n \left(1 - \int_0^{u_n} du_{n + 1}\right) \\
&= ~ \, P_n(u_1) - P_{n + 1}(u_1) \\
&= ~ \, \frac{u_1^{n-1}}{(n - 1)!} - \frac{u_1^n}{n!}~.
\end{align}
$$
This is an interesting exercise and a tidy result, but how does this relate to sampling from an exponential distribution?
An odd result
What is the probability of obtaining and odd-length decreasing sequence (OLDS) for a given $u_1$? Sum $S_n(u_1)$ over odd values of $n$ to get:
$$
\begin{align}
S_1(u_1) + S_3(u_1) + \ldots = 1 - u_1 + \frac{u_1^2}{2!} - \frac{u_1^3}{3!} + \ldots ~.
\end{align}
$$
Does this look familiar? Here's a big hint: the Taylor series expansion of $e^{-u_1}$ is
$$
\begin{equation}
e^{-u_1} = \sum_{n = 0}^\infty \frac{(-u_1)^n}{n!} = 1 - u_1 + \frac{u_1^2}{2!} - \frac{u_1^3}{3!} + \ldots~.
\end{equation}
$$
We now arrive at an interesting and useful result: A series of random numbers uniformly distributed over $(0, 1)$, starting with $u_1$, makes an OLDS with probability $e^{-u_1}$. In other words, if many decreasing sequences are generated that terminate with odd length, and only $u_1$ is retained in each case, then the collection of $u_1$ values will be a sample from the exponential distribution over $(0, 1)$.
So, we're on the right track. But how do we sample $e^{-x}$ over its entire domain from 0 to $\infty$?
A do-over
For a given value of $u_1$, the probability of an OLDS is $e^{-u_1}$. The probability of an OLDS when $u_1$ is in the infinitesimal range $(u_1, u_1 + du_1)$ is $du_1 e^{-u_1}$. Integration over $u_1$ gives the probability of an OLDS for any $u_1$: $\int_0^1 du_1 e^{-u_1} = 1 - e^{-1}$. It follows that the probability of an even-length decreasing sequence for any $u_1$ is $e^{-1}$. If $u_1$ is accepted as a random draw from the exponential distribution only when the length of the decreasing sequence is odd, then $e^{-1}$ represents the probability that a sequence is rejected. A rejected even-length sequence doesn't mean all is lost. It just means we start the process over, but with a small additional twist.
Suppose we encounter an even-length decreasing sequence in the first pass. Reject this sequence and start over by creating a new decreasing sequence with a freshly chosen value of $u_1$. If this new sequence has an odd length, accept the new $u_1$. The probability of rejecting the first sequence and accepting the second is $e^{-1} e^{-u_1} = e^{-(u_1 + 1)}$. Because $u_1$ is drawn from $(0, 1)$, a rejection followed by an acceptance samples from the exponential distribution in the interval $(1, 2)$. Similarly, the probability of accepting $u_1$ after two rejections is $e^{-(u_1 + 2)}$. And so on.
A complete recipe
The complete algorithm is shown below as a flow diagram. Each draw is initialized by choosing a random $x$ in the unit interval ($u_1$ in the discussion above), setting the initial sequence length to $n = 1$, and setting the initial rejection count to $k = 0$. In the diagram, $u$ and $u'$ represents, respectively, the previous and most recent random numbers. When a decreasing sequence of random numbers terminates with an odd length, the algorithm returns $x + k$.
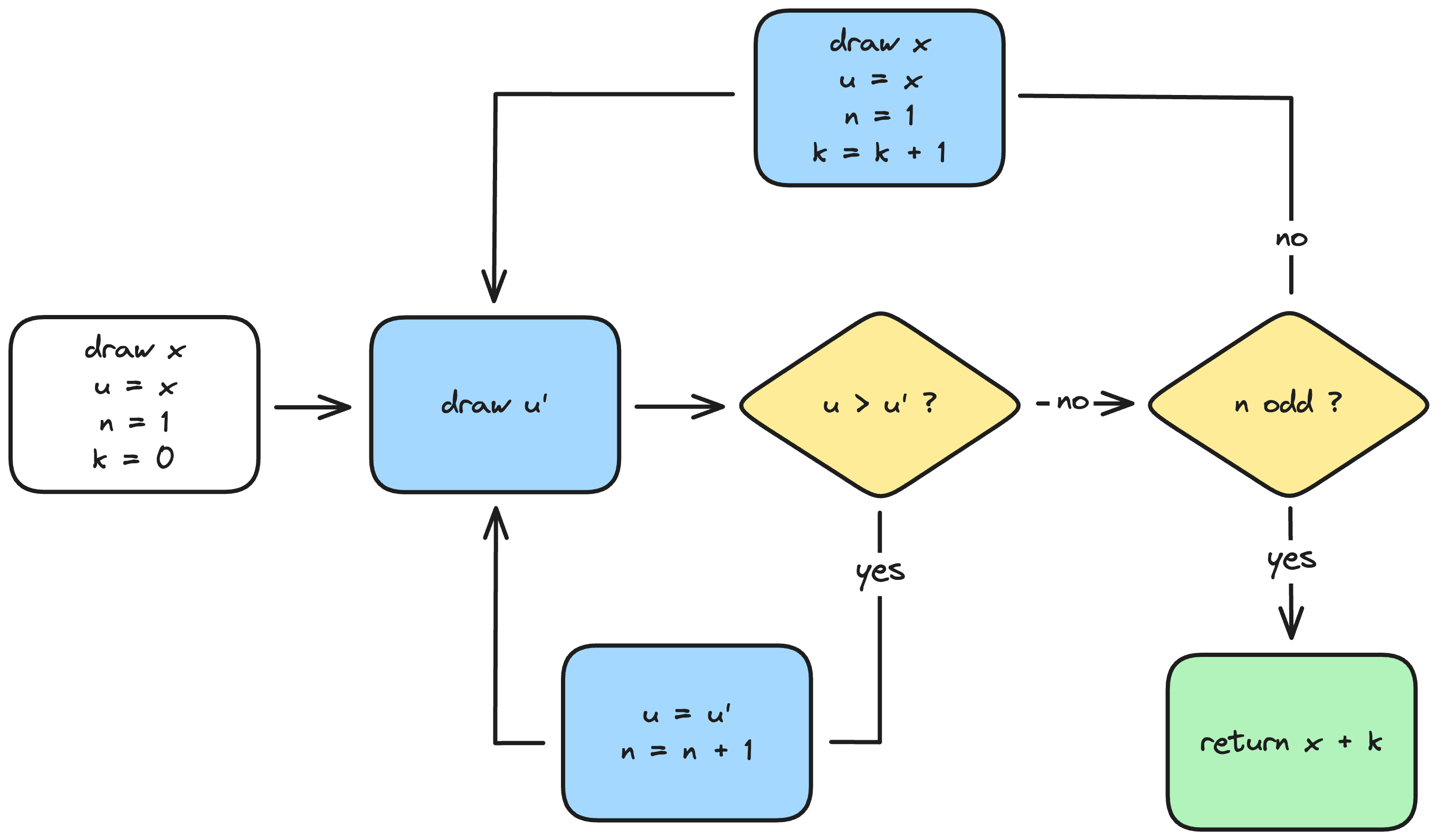
An Elixir implementation of von Neumann's algorithm can be found in this gist.
It's unlikely to generate long decreasing sequences or for there to be many rejections. It can be shown that the expected number of random draws before the algorithm returns is approximately 4.3. The standard technique for sampling from an exponential distribution is to compute $-\ln (1 - u)$, where $u$ is a uniform random number on $(0, 1)$. While von Neumann's approach is significantly less efficient, it avoids an explicit computation of a logarithm. Also, it's straightforward to show that the the algorithm can be adapted to any probability density of the form $a e^{-f(x)}$ for constant $a$.
Until next time, keep it random!
