How long is a satellite visible from the ground?

It's a clear, dark night. You look up and gaze at the stars, shining reminders that the universe is vast and wonderful. While you're peacefully basking in the light of distant suns, you notice one bright dot is out of place. It's moving. But no blinking lights, like we'd expect of an aircraft. Chances are, it's another invention of our modern age–a satellite. Think about that: an object that we puny humans created and then shot into space on a tower of fire.

When we're fortunate enough to spot a satellite, how long will it be visible? The geometry of the Earth and the satellite's orbit limit how much of the orbit can be seen from the ground. A satellite might first be visible when it ascends above the horizon, and then disappear after it crosses overhead and dips below the horizon in the opposite direction. With a few simplifying assumptions, a pinch of trig, and a smidge of orbital mechanics, these squishy statements can be made precise. I'll walk you through the steps. First, I'll lay out the basic geometry and key assumptions.

To a good approximation, the Earth is a sphere with radius $R \approx 6400\,{\rm km}$. The satellites we're likely to see from the ground have an altitude $h$ of hundreds of kilometers. For example, the International Space Station has an altitude of about $400\,{\rm km}$. Assume also that the satellite passes directly overhead, that the satellite's orbit is perfectly circular, and that the observer is located at sea level. All of these assumptions make the math a little easier. The diagram below shows the idealized geometry:

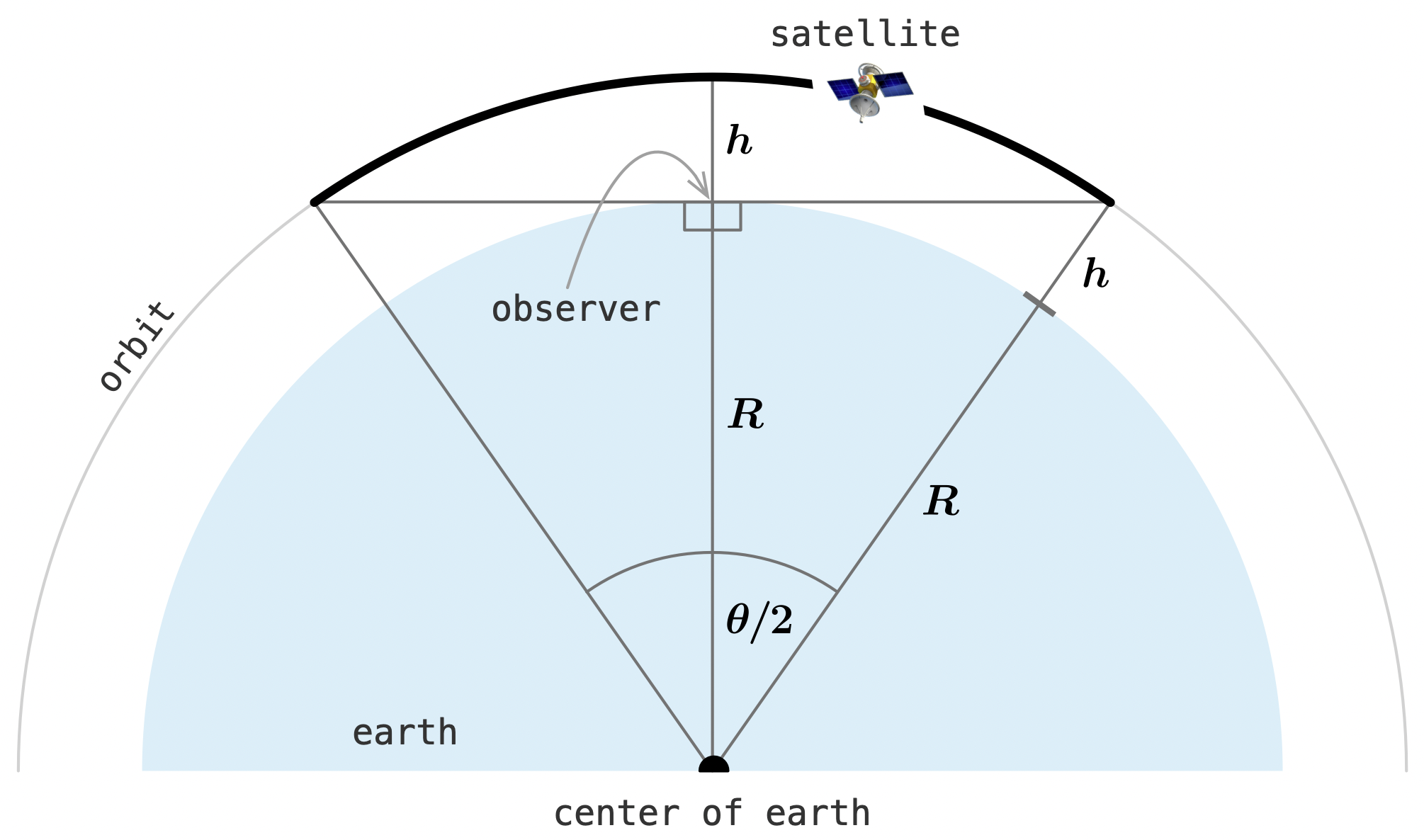
The satellite is visible only for the part of its orbit above the observer's horizon. This arc is shown as the bold section above. Measured from the center of the satellite's orbit (also the center of the Earth), $\theta$ is the angle subtended by the visible arc. The time for the satellite to complete one orbit is $P$, the satellite's orbital period. The duration $D$ for which the satellite is visible is $P$ times the fraction of the orbit in the visible arc, which is $\theta/2\pi$. So, we find that $D = P\theta/2\pi$. How is $\theta$ determined?

Connecting the ends of the visible arc is a line that is tangent to the Earth's surface and perpendicular to the line from the Earth's center to the observer. This line, together with the three lines from the center of the orbit, forms two equivalent right triangles, each with angle $\theta/2$, adjacent side $R$, and hypotenuse $R + h$, the orbital radius:

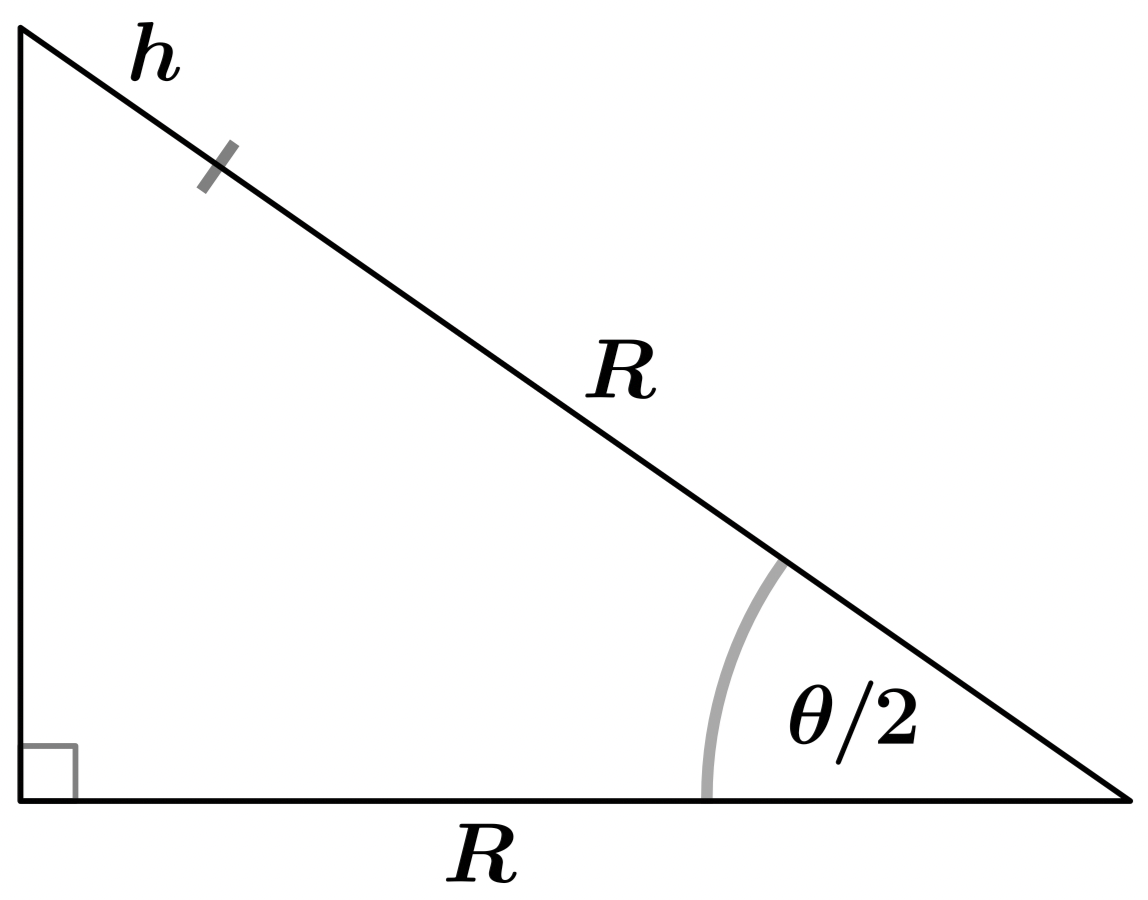
Here's where the trig comes in: notice that

$$
\cos(\theta/2) = \frac{R}{R + h}~,
$$

When $h$ is less than about $1000\,{\rm km}$, there is a handy approximation for $\theta$ that is within 10% of the exact result (obtained after Taylor expanding both sides of the above equation):

$$
\theta \approx \sqrt{\frac{8h}{R}}~.
$$

For an orbital altitude of $h = 400\,{\rm km}$, the fraction of the orbit for which the satellite is visible is $\theta/2\pi \approx 0.11$.

From Kepler's third law, the period $P$ of the satellite's orbit is given by

$$
\frac{P}{2\pi} = \sqrt{\frac{(R + h)^3}{GM}}~,
$$

where $M\approx 6\times 10^{24}\,{\rm kg}$ is the mass of the Earth, $G \approx 6.67\times 10^{-11}\,{\rm m^3\,kg^{-1}\,s^{-2}}$ is the gravitational constant, and $R+h$ is the satellite's orbital radius.

Now let's put all of this together. If only the smallest power of $h$ is retained, the visible duration is approximately

$$
D = \frac{P\theta}{2\pi}\approx \sqrt{\frac{8hR^2}{GM}}~.
$$

When $h = 400\,{\rm km}$, this is about 10 minutes. This is an optimistic number. If the satellite doesn't fly directly overhead, or if there are obstructions near the horizon, the duration will be shorter, probably only a few minutes typically.

That's it! I hope you enjoyed learning a bit about satellite orbits. And I hope you're inspired to do some satellite spotting.